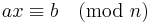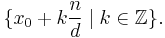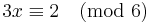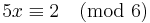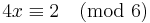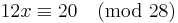Linear congruence theorem
In modular arithmetic, the question of when a linear congruence can be solved is answered by the linear congruence theorem. If a and b are any integers and n is a positive integer, then the congruence
has a solution for x if and only if b is divisible by the greatest common divisor d of a and n (denoted by gcd(a,n)). When this is the case, and x0 is one solution of (1), then the set of all solutions is given by
In particular, there will be exactly d = gcd(a,n) solutions in the set of residues {0,1,2,...,n-1}.
Contents |
Example
For example, examining the equation ax ≡ 2 (mod 6) with different values of a yields
Here d = gcd(3,6) = 3 but since 3 does not divide 2, there is no solution.
Here d = gcd(5,6) = 1, which divides any b, and so there is just one solution in {0,1,2,3,4,5}: x=4.
Here d = gcd(4,6) = 2, which does divide 2, and so there are exactly two solutions in {0,1,2,3,4,5}: x=2 and x=5.
Solving a linear congruence
In general solving equations of the form:
If the greatest common divisor d = gcd(a, n) divides b, then we can find a solution x to the congruence as follows: the extended Euclidean algorithm yields integers r and s such ra + sn = d. Then x = rb/d is a solution. The other solutions are the numbers congruent to x modulo n/d.
For example, the congruence
has 4 solutions since gcd(12, 28) = 4 divides 20. The extended Euclidean algorithm gives (-2)*12 + 1*28 = 4, i.e. r = -2 and s = 1. Therefore, one solution is x = -2*20/4 = -10, and -10 = 4 modulo 7. All other solutions will also be congruent to 4 modulo 7. Since the original equation uses modulo 28, the entire solution set in the range from 0 to 27 is x = {4,11,18,25}
System of linear congruences
By repeatedly using the linear congruence theorem, one can also solve systems of linear congruences, as in the following example: find all numbers x such that
- 2x ≡ 2 (mod 6)
- 3x ≡ 2 (mod 7)
- 2x ≡ 4 (mod 8).
By solving the first congruence using the method explained above, we find x ≡ 1 (mod 3), which can also be written as x = 3k + 1. Substituting this into the second congruence and simplifying, we get
- 9k ≡ −1 (mod 7).
Solving this congruence yields k ≡ 3 (mod 7), or k = 7l + 3. It then follows that x = 3 (7l + 3) + 1 = 21l + 10. Substituting this into the third congruence and simplifying, we get
- 42l ≡ −16 (mod 8)
which has the solution l ≡ 0 (mod 4), or l = 4m. This yields x = 21(4m) + 10 = 84m + 10, or
- x ≡ 10 (mod 84)
which describes all solutions to the system.